Preferential Bayesian optimization (PBO) is a variant of Bayesian optimization that observes relative preferences (e.g., pairwise comparisons) instead of direct objective values, making it especially suitable for human-in-the-loop scenarios. However, real-world optimization tasks often involve inequality constraints, which existing PBO methods have not yet addressed. To fill this gap, we propose constrained preferential Bayesian optimization (CPBO), an extension of PBO that incorporates inequality constraints for the first time. Specifically, we present a novel acquisition function for this purpose. Our technical evaluation shows that our CPBO method successfully identifies optimal solutions by focusing on exploring feasible regions. As a practical application, we also present a designer-in-the-loop system for banner ad design using CPBO, where the objective is the designer’s subjective preference, and the constraint ensures a target predicted click-through rate. We conducted a user study with professional ad designers, demonstrating the potential benefits of our approach in guiding creative design under real-world constraints.
We aim to solve a constrained optimization problem of the form:
\[ x^* = \arg\max_{x \in \mathcal{X}} f(x) \quad \text{s.t.} \quad c(x) \geq \lambda \]
where \( f(x) \) is a black-box objective function observed via relative preferences (e.g., a designer’s subjective preference), and \( c(x) \) is a black-box constraint function (e.g., design performance) with a threshold \( \lambda \). CPBO extends PBO by incorporating such inequality constraints.
To implement CPBO, we propose a new acquisition function called EUBOC (Expected Utility of the Best Option with Constraints), which integrates EUBO — one of the state-of-the-art acquisition functions for PBO — with the idea of Expected Improvement with Constraints (EIC):
\[ \text{EUBOC}(x^{(i)}, x^{(j)}) = \mathcal{P}(c(x^{(i)}) \geq \lambda,\, c(x^{(j)}) \geq \lambda) \cdot \text{EUBO}(x^{(i)}, x^{(j)}). \]
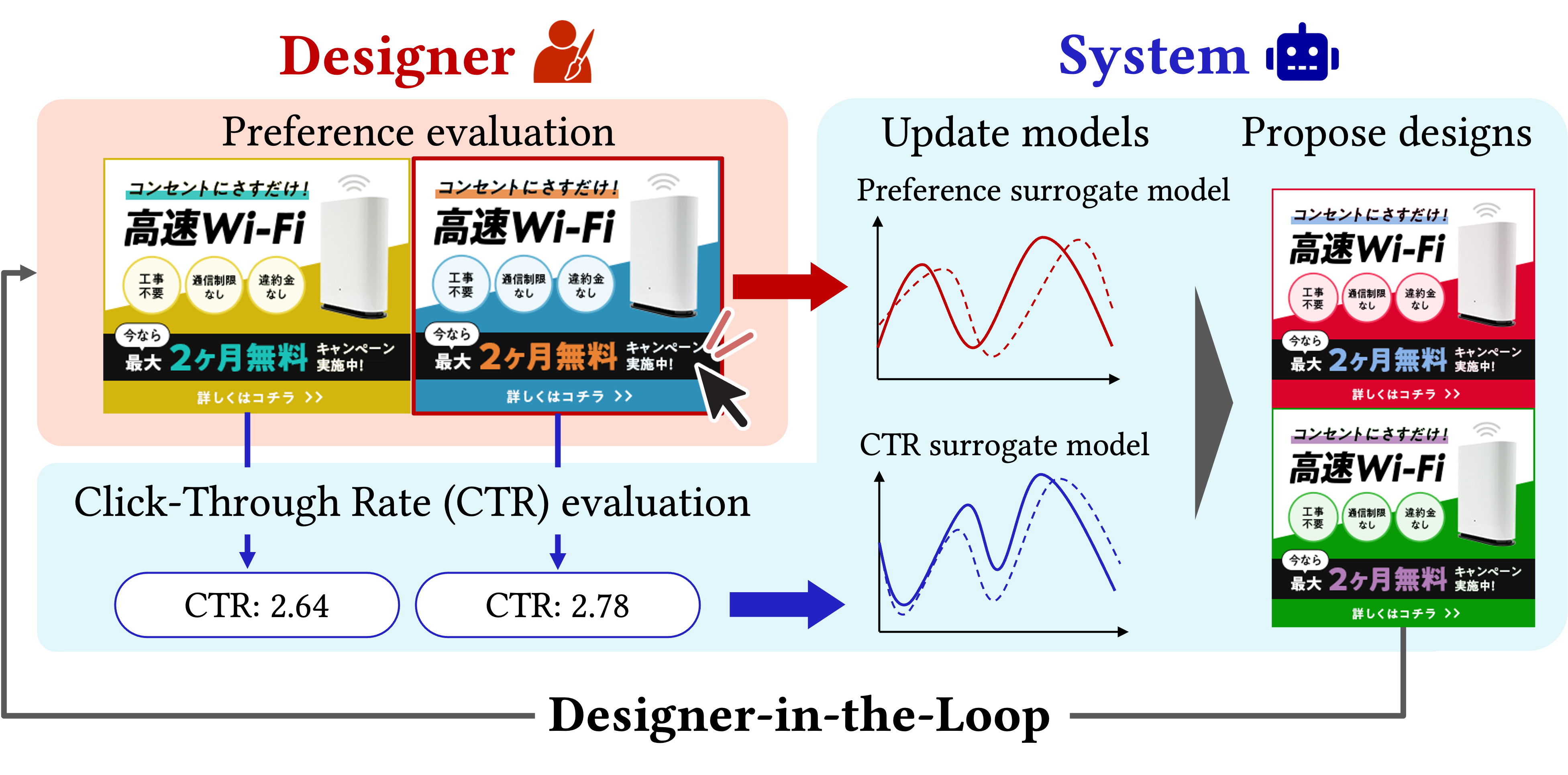
We apply our CPBO technique to a practical setting of banner ad design. In this framework, a designer iteratively selects preferred candidates among ad design variations, while the system ensures that the predicted click-through rate (CTR) satisfies a constraint.
The system maintains surrogate models for both preference (based on designer's selections) and CTR (based on a prediction model). At each step, a new pair of designs is proposed by maximizing the EUBOC acquisition function, enabling optimization that respects both subjective aesthetics and business goals.
@inproceedings{iwai2025cpbo,
author = {Iwai, Koki and Kumagae, Yusuke and Koyama, Yuki and Hamasaki, Masahiro and Goto, Masataka},
title = {Constrained Preferential Bayesian Optimization and Its Application in Banner Ad Design},
booktitle = {Proceedings of the Thirty-Fourth International Joint Conference on Artificial Intelligence, {IJCAI-25}},
year = {2025}
}